Zero Limits: The Secret Hawaiian System for Wealth, Health, Peace, and More Audible Audiobook – Unabridged Joe Vitale (Author, Narrator), Ihaleakala Hew Len (Author, Narrator), Gildan Media, LLC (Publisher) 1,488 ratings See all formats and editions. What is Zero Limits? Zero Limits Montessori House of Children is dedicated towards catering to the unique needs of your little child. Every child has a love to learn new things and our duty as an educator is to ensure that this flame of love burns brightly.
ZeroLimits.org is proud to offer high quality self-help books and resources such as videos, inspirational quotes, copyright-free self-improvement books, health & fitness books and money & business books in the public domain, several of which can be read for free, right here on ZeroLimits.org.
- Zero Limits: The Secret Hawaiian System For Wealth, Health, Peace And More is a self-improvement book which employs a breakthrough approach. It helps people who are overworked, overstressed and are bound by self-imposed limitations which manifest in the form of disease, chaos and poverty.
- The simple method of saying four specific phrases, while meditating on your problem and connecting with your idea of a higher power, is enough to start wipin.
- Altra was founded with a desire to find a better shoe for road and trail running. Experience the difference of our FootShape™ and ZeroDrop™ design.
The public domain books on offer can also be downloaded for a small fee if you would like the right to not only use them for your own personal upliftment but to also help others by selling them, giving them away, turning them into audio books, or even better still, use the content for ideas and publish your own unique book! In fact, they can be used for any commercial project as they have no usage restrictions in the USA, i.e. zero limits!
Note that there are many public domain resources available on the Internet but that many of these have been edited or modified and are therefore no longer copyright-free. The public domain books for sale on our site are all scanned copies of original books that are now in the public domain in the USA and that we have in some cases had to acquire at great cost. They are available in an editable word document format together with a pdf file and flat e-cover in five different sizes.
We are confident that between our self-help books, articles, inspirational quotes and videos you will pick up many golden nuggets. Please bookmark us and visit us often as we will be adding new content on a very regular basis. And, don’t forget to sign up for our free newsletter!
You should read Limits (An Introduction) first
Quick Summary of Limits
Sometimes we can't work something out directly ... but we can see what it should be as we get closer and closer!
Example:
(x2 − 1)(x − 1)
Let's work it out for x=1:
(12 − 1)(1 − 1) = (1 − 1)(1 − 1) = 00
Now 0/0 is a difficulty! We don't really know the value of 0/0 (it is 'indeterminate'), so we need another way of answering this.
So instead of trying to work it out for x=1 let's try approaching it closer and closer:
Example Continued:
| x | (x2 − 1)(x − 1) |
| 0.5 | 1.50000 |
| 0.9 | 1.90000 |
| 0.99 | 1.99000 |
| 0.999 | 1.99900 |
| 0.9999 | 1.99990 |
| 0.99999 | 1.99999 |
| ... | ... |
Now we see that as x gets close to 1, then (x2−1)(x−1) gets close to 2
We are now faced with an interesting situation:
- When x=1 we don't know the answer (it is indeterminate)
- But we can see that it is going to be 2
We want to give the answer '2' but can't, so instead mathematicians say exactly what is going on by using the special word 'limit'
The limit of (x2−1)(x−1) as x approaches 1 is 2
And it is written in symbols as:
limx→1x2−1x−1 = 2
So it is a special way of saying, 'ignoring what happens when we get there, but as we get closer and closer the answer gets closer and closer to 2'
As a graph it looks like this: So, in truth, we cannot say what the value at x=1 is. But we can say that as we approach 1, the limit is 2. |
Evaluating Limits
'Evaluating' means to find the value of (think e-'value'-ating)
In the example above we said the limit was 2 because it looked like it was going to be. But that is not really good enough!
In fact there are many ways to get an accurate answer. Let's look at some:
1. Just Put The Value In
The first thing to try is just putting the value of the limit in, and see if it works (in other words substitution).
Example:
| limx→1x2−1x−11 x^2~−1/x−1 --> | (1−1)(1−1) = 00 |
No luck. Need to try something else.
2. Factors
We can try factoring.
Example:
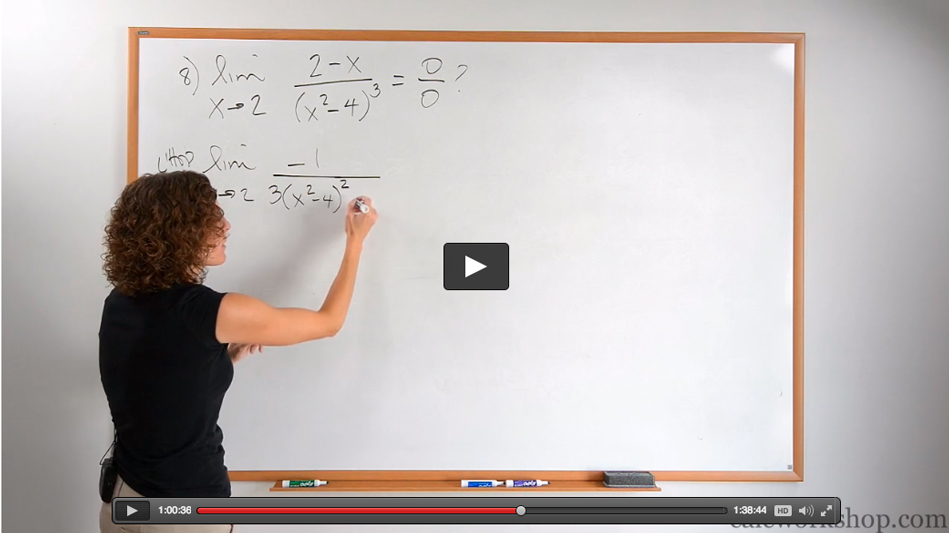
limx→1x2−1x−1
By factoring (x2−1) into (x−1)(x+1) we get:
1] x^2~-1/x-1 = LIM[x->1] (x-1)(x+1)/(x-1)-->
 1] (x+1) -->
1] (x+1) -->Zero Limits Dvd
Now we can just substitiute x=1 to get the limit:
 1] (x+1) = 1+1 = 2 -->
1] (x+1) = 1+1 = 2 -->3. Conjugate

For some fractions multiplying top and bottom by a conjugate can help.
| The conjugate is where we change the sign in the middle of 2 terms like this: |

Here is an example where it will help us find a limit:
| 4] 2-SQRx/4-x --> | Evaluating this at x=4 gives 0/0, which is not a good answer! |
So, let's try some rearranging:
| Multiply top and bottom by the conjugate of the top: | 2−√x4−x × 2+√x2+√x |
| Simplify top using (a+b)(a−b) = a2 − b2: | |
| Simplify top further: | 4−x(4−x)(2+√x) |
| Cancel (4−x) from top and bottom: |
So, now we have:
Done!
4. Infinite Limits and Rational Functions
| A Rational Function is one that is the ratio of two polynomials: | |
| For example, here P(x) = x3 + 2x − 1, and Q(x) = 6x2: | x3 + 2x − 16x2 |
By finding the overall Degree of the Function we can find out whether the function's limit is 0, Infinity, -Infinity, or easily calculated from the coefficients.
Read more at Limits To Infinity.
5. L'Hôpital's Rule
L'Hôpital's Rule can help us evaluate limits that at first seem to be 'indeterminate', such as 00 and ∞∞.
Read more at L'Hôpital's Rule.
Zero Limits Performance
6. Formal Method
Zero Limits 3
The formal method sets about proving that we can get as close as we want to the answer by making 'x' close to 'a'.
Zero Limits Ventures
Read more at Limits (Formal Definition)